What, if anything, is Gibbs?

So there is this thing I noticed about chemistry when I took my first intro class (11 years? Holy crap!). I’m certainly not the first one to notice it, but the way that atoms arrange themselves in the shapes they do is really amazingly elegant.

In essence, every chemical reaction can be written as . That is, something (A) changes into something else (B), which can (in principle) turn back into A. As long as nothing nuclear happens, the atoms in A are the same as those in B; we therefore call A and B ‘states’ of those atoms. Because A turns into B at the same time as B turns into A, there will always be a little bit of both.

If you start with A and let enough time pass, eventually enough A will be used up that the rate at which you get more B drops. At the same time, enough B will be produced that the rate at which A is produced rises. When these to rates are equal, they cancel and the relative amount of A and B stays the same until something else changes. We call this ‘dynamic equilibrium’, and the question “how much do I have at equilibrium?” makes up fully half of chemistry (the other half being “how long does it take?” or, alternately, “do I have time to grab lunch?”)

In order to understand how sets of atoms end up in one state or the other (and therefore if you have more A or more B), we need to know two things about energy. First: energy is change, actual or potential, in the world. If you throw a ball, it has energy because the ball is changing its physical location in the world. If you push on a spring, it has energy because it could move something else or itself when you release it. Energy is nothing more and nothing less than this. Second: the second law of thermodynamics (simplified)- unless there is an outside influence, energy and matter will disperse over time.

The reason that I say that this is elegant is that apart from a couple of constant numbers and some math, energy is everything that you need to understand in order to understand how much of A and B you have at equilibrium. Don’t believe me? The answer to the “how much” question is a simple arithmetic calculation from a number that we call K_eq. The equation below is the legit, unabridged equation for K_eq, with notes detailing what everything is:

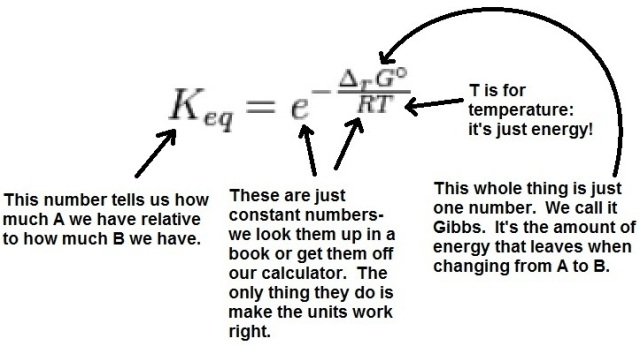
There you have it: K_eq in terms of a couple of constant numbers and two other things which are both energy.

But what is Gibbs, exactly? What does it do? Very few states contain exactly the same amount of potential energy. Odds are that A and B have different amounts, so let’s say A has more. When A changes to B, some energy is left over and can leave to actually change something out in the world. Gibbs is simply how much A can change the world by turning into B (idea of Gibbs has many names- energy change, free energy, relative stability, etc.; I have it labeled “Energy Change” in the simple graph below but it’s all the same).

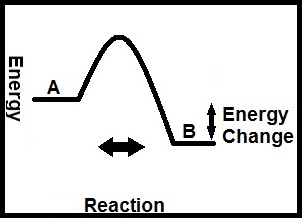
So what did I mean by energy dispersing? When A turns into B, the energy in A goes from a confined state (stuck entirely in A) to dispersed (some of it confined to B, some of it out changing the world). At the same time, some of the energy out in the world (represented by the temperature) disperses- it goes from being stuck entirely in the world to being dispersed (ever so slightly) with most still changing the world, but a tiny bit changing B back into A, restoring A’s potential to change the world at a later time.

Of course if things are different, say B has more energy than A, it all reverses and B changes into A spontaneously and energy from the world is required to change A back to B. But the only important things are these two quantities of energy- the relative stability of your two states and how much work you do to change things. That’s all you need to know to tell which way things will change. Elegant.